R을 이용한 통계분석(잔차 분석)

앞의 과정에서 데이터 간의 관계를 선으로 표현하는 회귀분석을 살펴보았습니다.
이후 더 정확한 회귀선을 추정하기 위해서는 잔차분석이 이루어 져야 합니다.
아래의 3가지 과정을 통해 알아보겠습니다.

• 추정된 회귀선의 잔차 분석
  • 잔차의 정규성
  • 잔차의 독립성
  • 잔차의 등분산성

> 잔차의 정규성 
ggplot(NULL) +
  geom_histogram(aes(x=Reg1$residuals),bins=100) +
  theme_bw() +
  xlab("Residuals")


> 잔차의 등분산성 
ggplot(NULL) +
  geom_point(aes(Reg1$fitted.values,y=Reg1$residuals),
             alpha=0.4,col="grey20")+
  geom_smooth(aes(Reg1$fitted.values,y=Reg1$residuals))+
  geom_hline(yintercept = 0,linetype="dashed",col="red",alpha=0.8)+
  theme_bw()


> 잔차의 독립성
ggplot(NULL) +
  geom_point(aes(x=1:length(Reg1$residuals),y=Reg1$residuals),
             alpha=0.4,col="grey20")+

  geom_hline(aes(yintercept =mean(Reg1$residuals)),
             linetype="dashed",col="red",alpha=0.8)+
  theme_bw()

• 종합결과

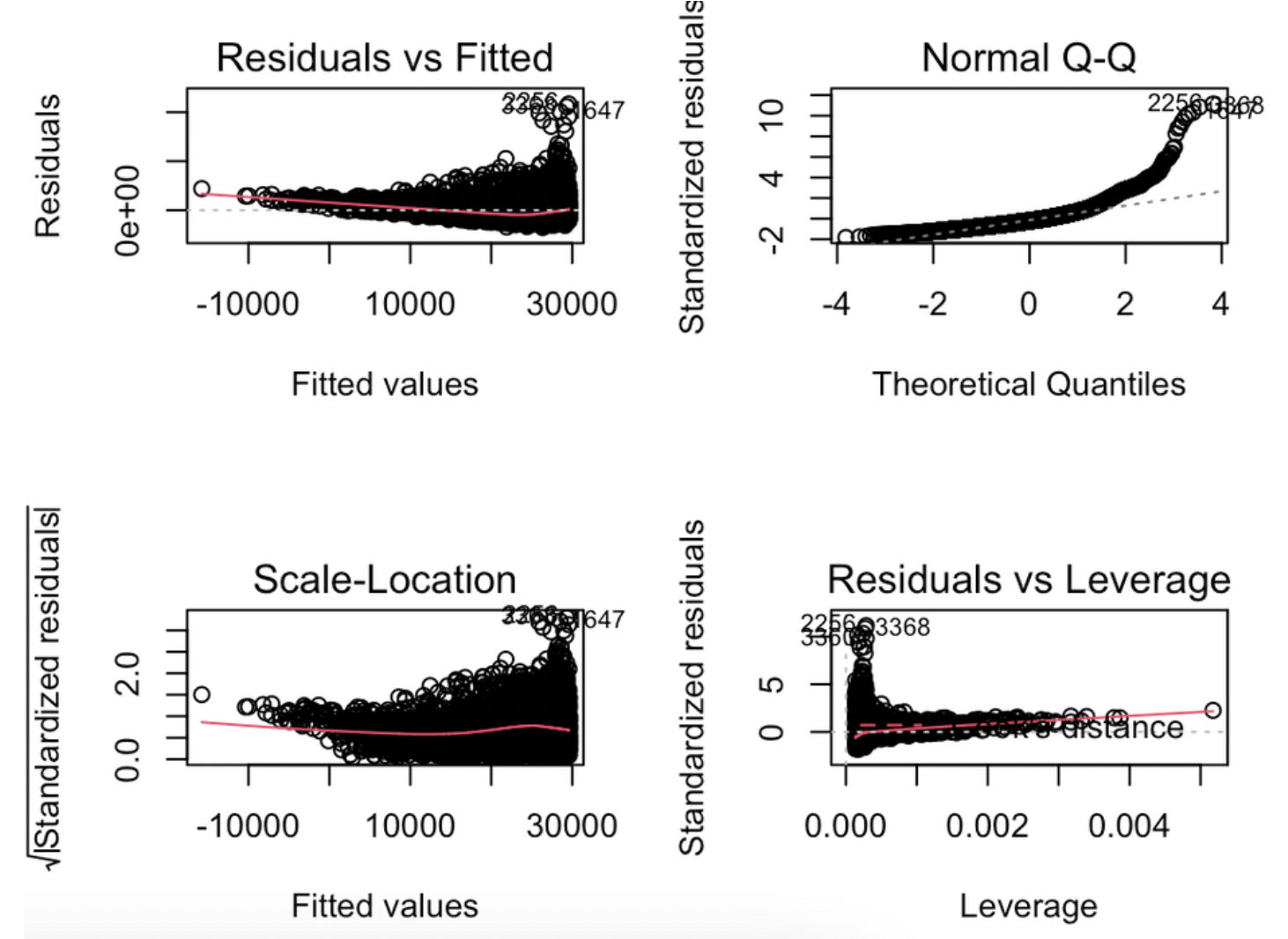
결과해석

• 잔차는 정규성을 띄지 않고, 추정된 휘귀선은 등분산성을 만족하지 못합니다.(x축의 위치에 상관없이 일정한 수준의 분산과 패턴이 존재해야합니다.)
• 추정된 휘귀선은 등분산성을 만족하지 못합니다.(x축의 위치에 상관없이 일정한 수준의 분산과 패턴이 존재해야합니다.)
• 종합결과
  - 1행1열 : 순수하게 residual이 y축
  - 2행1열 : 표준화잔차가 y축
  - 1행2열 : 잔차의 정규성을 확인하는 Normal QQplot
  -2행2열 : 영향점을 표시